Diện tích tam giác rất quan trọng đi suốt chương trình học của chúng ta. Chúng ta cần nắm rõ để áp dụng cho chính xác. Trong bài viết Gia sư Điểm 10 tổng hợp công thức tính diện tích tam giác dễ hiểu và được sử dụng nhiều nhất để bạn có thể áp dụng ngay trong các bài thi.

1. Diện tích tam giác cơ bản
Tam giác thường là tam giác có độ dài 3 cạnh khác nhau và số đo 3 góc khác nhau các cạnh và các góc hợp thành 1 tam giác.

>>Xem thêm: 7 hằng đẳng thức đáng nhớ.
2. Tính diện tích tam giác khi biết 1 góc

>>Xem thêm: Giải phương trình bậc nhất đơn giản.
3. Diện tích tam giác theo công thức Heron

4. Diện tích theo bán kính đường tròn ngoại tiếp

>>Xem thêm: Định lý Pytago giúp tính các cạnh của tam giác vuông
5. Diện tích theo bán kính đường tròn nội tiếp


6. Diện tích tam giác vuông
Tam giác vuông là tam giác có một góc bằng 90 độ(Góc vuông).

Tam giác ABC vuông tại B(Có góc B = 90 độ), a, b là độ dài hai cạnh góc vuông:
Áp dụng công thức tính diện tích thường cho diện tích tam giác vuông với độ dài hai canh góc vuông lần lượt là a và b.
Ta có công thức tính diện tích tam giác vuông:

7. Diện tích tam giác cân
Tam giác cân là tam giác có hai cạnh bên bằng nhau hoặc hai góc ở đáy bằng nhau.
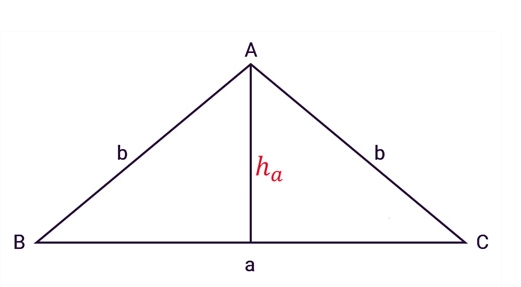
Tam giác cân ABC có ba cạnh, a là độ dài cạnh đáy, b là độ dài hai cạnh bên, ha là đường cao (Cạnh ha vuông góc với cạnh a)từ đỉnh A như hình vẽ:
Áp dụng công thức tính diện tích thường, ta có công thức tính diện tích tam giác cân:

>>Xem thêm: Tổng hợp kiến thức về tam giác đều bao gồm diện tích, tính chất, cách chứng minh.
8. Diện tích tam giác đều
Tam giác điều là tam giác có 3 cạnh bằng nhau hoặc 3 góc bằng nhau và mỗi góc bằng 60 độ.
Tam giác đều ABC có ba cạnh bằng nhau, a là độ dài các cạnh như hình vẽ:

Với diện tích tam giác đều ta chỉ cần áp dụng công thức:
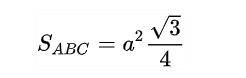
9. Diện tích tam giác vuông cân
Tam giác ABC vuông cân tại A, a là độ dài hai cạnh góc vuông:
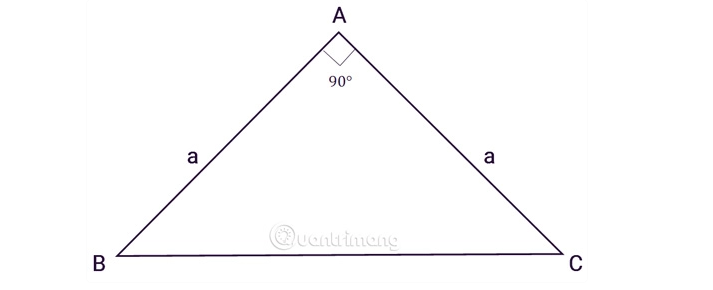
Áp dụng công thức tính diện tích vào tam giác vuông cân ta có:

>>Xem thêm: Tổng hợp kiến thức về lũy thừa lớp 6.
10. Diện tích hệ trục tọa độ xOy
Ngoài ra lớp 10 chúng ta sẽ tính diện tích tam giác theo hệ trục tọa độ Oxyz. Như vậy ngoài một số công thức tính diện tích tam giác thông thường chúng ta còn tính diện tích tam giác trong hệ trục tọa độ Oxyz.