Giasudiem10 xin giới thiệu tài liệu tới quý thầy cô giáo và các em học sinh lớp 8 ôn tập phần bài tập Định lý Talet trong tam giác trong môn Toán. Bài viết có đầy đủ lý thuyết và tuyển chọn các dạng bài tập của Định lý. Và các bài tập này đều sẽ có lời giải tổng hợp và bài tập có đáp án (và lời giải). Giúp học sinh có thêm nguồn tài liệu ôn tập, củng cố kiến thức và hiểu biết. Và là một nền tảng vững chắc cho kỳ thi Toán sắp tới. Chúc các em học sinh đạt hiệu quả cao trong học tập và hoàn thành tốt mục tiêu của mình.
Mục Lục
1. Định lí Ta lét trong tam giác là gì?
Định lí Ta-lét hay còn được gọi là định lý Thales, là một trong những định lý có vai trò rất quan trọng trong lĩnh vực hình học nói riêng. Và trong Toán học nói chung, định lý này có tên gọi được đặt theo tên của một nhà Toán học đến từ Hy Lạp, ông tên là Thales.
1.1 Định nghĩa định lí Ta lét trong tam giác
1.1.1 Tỉ số của hai đường thẳng
a) Định nghĩa tỉ số hai đường thẳng như sau:
+ Tỉ số của hai đoạn thẳng chính là tỉ số độ dài của chúng theo cùng một đơn vị đo.
+ Tỉ số của hai đoạn thẳng CD và AB được kí hiệu là CD/AB.
+ Chú ý: Tỉ số của hai đoạn thẳng là không phụ thuộc vào các chọn đơn vị đo
b) Ví dụ minh họa:
- Cho đoạn thẳng AB = 20 cm; đoạn thẳng CD = 40 cm thì ⇒ AB/CD = 20/40 = 1/2.
- Cho đoạn thẳng AB = 2 m; CD = 4 m thì AB/CD = 2/4 = 1/2.
1.1.2 Đoạn thẳng tỉ lệ
Định nghĩa được phát biểu như sau:
+ Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng A’B’ và C’D’ nếu có tỉ lệ thức.
+ Tổng quát:
1.2.3 Định lý Ta-lét trong tam giác
Định lý Ta-lét được phát biểu như sau: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
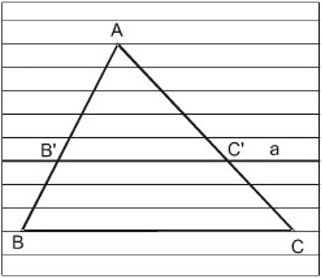
Tổng quát : Δ ABC, B’C’//BC; B’ ∈ AB, C’ ∈ AC
Ta có:
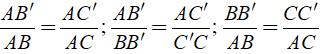
1.2 Định lý Ta-lét đảo
+ Định lý Ta lét trong tam giác là một định lý mang tính chất 2 chiều, đó là chiều thuận và chiều đảo ngược.
+ Định lý Ta lét đảo được phát biểu như sau:
Nếu trong một tam giác, một đường thẳng cắt 2 cạnh của tam giác đó và định ra trên 2 cạnh được cắt những đoạn thẳng tương ứng tỉ lệ với nhau thì đường thẳng đó sẽ song song với cạnh còn lại.
Trong △ABC,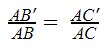 
thì ta sẽ có B’C’ // BC.
+ Định lý Ta lét thuận và Ta lét đảo có thể được áp dụng được đối với 3 trường hợp hình vẽ mô tả dưới đây:
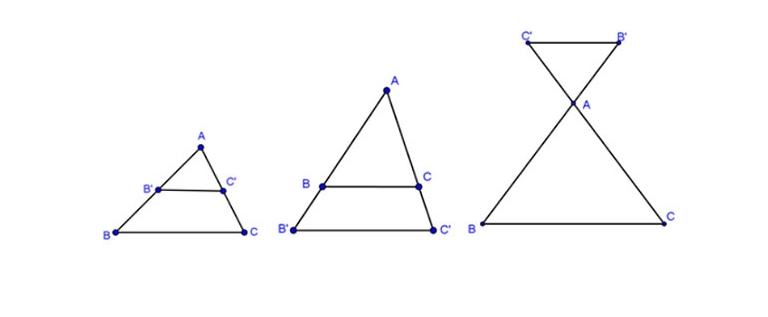
2. Hệ quả của định lý Ta lét
2.1 Hệ quả 1
Hệ quả 1 của định lí Ta-lét trong tam giác được phát biểu như sau:
Khi một đường thẳng song song với một cạnh của một tam giác có sẵn và đồng thời cắt 2 cạnh còn lại
=> Sẽ tạo ra được một tam giác mới có ba cạnh tỉ lệ với ba cạnh của tam giác đã được cho trước.
Trong △ABC, đường thẳng DE // BC thì ta sẽ có:
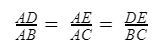
Đặc biệt, hệ quả 1 của định lý Ta-lét vẫn đúng đối với trường hợp như: Một đường thẳng a song song với 1 cạnh của tam giác đã cho trước và nó cắt 2 cạnh còn lại của tam giác khi kéo dài.
2.2 Hệ quả 2
Hệ quả 2 của định lý Ta lét được phát biểu như sau: Khi một đường thẳng cắt ngang 2 cạnh của một tam giác đã cho trước và song song với cạnh còn lại thì sẽ tạo ra được 1 tam giác mới và tam giác này đồng dạng với tam giác đã được cho trước đó.
2.3 Hệ quả 3
Hệ quả 3 của định lí Ta lét trong tam giác được biết đến là một định lý Ta lét mở rộng. Hệ quả 3 được phát biểu như sau:
Khi ba đường thẳng đồng quy thì sẽ chắn trên 2 đường thẳng song song những cặp đoạn thẳng tỉ lệ.
3.Các dạng toán được áp dụng về định lý Ta-lét trong tam giác
Dạng 1: Tính tỉ số hai đoạn thẳng và chia đoạn thẳng theo tỉ số cho trước
1) Sử dụng định nghĩa tỉ số của hai đoạn thẳng.
2) Một điểm C thuộc đoạn thẳng AB (hoặc thuộc đường thẳng AB) thì điểm C được gọi là chia đoạn thẳng AB theo tỉ số m/n, tỉ số này khác 1 (trong đó m, n là các số dương) nếu ta có: CA/CB =m/n.
3. Sử dụng kĩ thuật đại số hóa hình học.
4. Lập tỉ lệ thức giữa các đoạn thẳng tỉ lệ rồi áp dụng tính chất của dãy tỉ số bằng nhau.
Dạng 2: Tính độ dài đoạn thẳng. Dựng đoạn thẳng tỉ lệ thứ tư
1. Dạng bài tính độ dài đoạn thẳng có một số dạng dưới đây:
+ Áp dụng định lí Ta-lét trong tam giác để lập hệ thức của các đoạn thẳng tỉ lệ.
+ Xác định ra đường thẳng song song với một cạnh của tam giác.
+ Thay số vào hệ thức rồi giải phương trình.
2. Dạng bài dựng đoạn thẳng tỉ lệ thứ tự
Trong bốn đoạn thẳng tỉ lệ. Dựng đoạn thẳng thứ tự khi biết độ dài của ba đoạn kia:
+ Đặt ba đoạn thẳng trên hai cạnh của một góc.
+ Dựng đường thẳng song song để xác định đoạn thẳng thứ tư.
Dạng 3: Chứng minh các hệ thức hình học
1. Xác định đường thẳng song song với một cạnh của tam giác.
2. Áp dụng định lí Ta-lét để lập ra hệ thức của các đoạn thẳng tỉ lệ.
3. Sử dụng các tính chất của tỉ lệ thức hoặc cộng theo vế các đẳng thức hình học.
Dạng 4: Vẽ thêm đường thẳng song song để tính tỉ số hai đoạn thẳng
1. Vẽ thêm đường thẳng song song.
2. Sử dụng kĩ thuật đại số hóa hình học.
3. Áp dụng định lí Ta-lét.
3. Bài tập
3.1 Bài tập SGK
Bài 5 (SGK trang 59) tìm x :
Hình 7a :
Trong ΔABC, ta có :
MM // BC (gt)
=> AM/AB = AN/AC Hay 4/AB = 5/8,5 =>AB = 6,8
Mà : AB = AM + MB (M nằm giữa A và B)
6,8 = 4 + x
=> x = 6,8 – 4 = 2,8
Hình 7b : Giải tương tự ta được x = 6,3
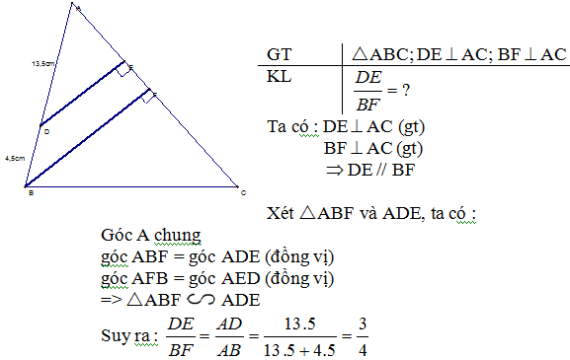
Bài 9 trang 63:
Cho trước tam giác ABC và điểm D trên cạnh AB, sao cho đoạn thẳng AD = 13,5cm, đoạn thẳng BD = 4,5cm. Hãy tính tỉ số các khoảng cách từ D và B đến AC.
Lời giải:
Cách 1:
Cách 2:
Ta có :
DE vuông góc AC (gt)
BF vuông góc AC (gt)
=> DE // BF
=> DE / BF = AD / AB = 13.5 / (13.5 + 4.5) = 3/4
3.2 Bài tập nâng cao khác
Bài 1: Cho một đoạn thẳng AB:
a) Trên đoạn thẳng AB lấy điểm C sao cho CA/CB = 3/2 . Hãy tính độ dài đoạn thẳng CB.
b) Trên tia đối của tia BA hãy lấy điểm D sao cho DA/DB = 3/2 . Hãy tính độ dài đoạn CD.
Gợi ý giải:
a) Từ giả thiết ta có:
với t > 0
Nên AB = 10 cm = CA + CB = 5t ⇔ t = 2
Vậy CB = 4 cm
b) Từ giả thiết ta có:
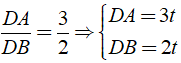
Mặt khác điểm D thuộc tia đối của tia BA nên DA > DB
Do đó AB = 10 cm = DA – DB = 3t – 2t ⇔ t = 10 cm
Vậy DB = 20 cm.
Bài 2: Tính giá trị của x trong hình vẽ cho trước:
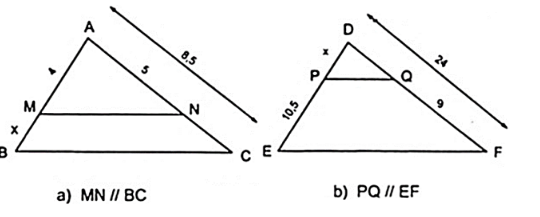
Gợi ý giải:
a) Sử dụng định lí Ta – lét vào tam giác ABC, ta có MN//BC
Ta có: AM/AB = AN/AC ⇒ AM/(AB – AM) = AN/(AC – AN) ⇔ AM/BM = AN/NC
Hay 4/x = 5/3,5 ⇒ x = 4.3,5/5 = 2,8cm
Vậy x = 2,8cm.
b) Áp dụng định lí Ta – lét vào tam giác DEF có PQ//EF
Ta có: PE/DE = QF/DF ⇒ PE/(DE – PE) = QF/(DF – QF)
10,5/x = 9/(24 – 9) ⇒ x = 10,5.15/9 = 17,5 cm
Vậy x = 17,5 cm
Trên đây giasudiem10 đã giới thiệu tới các bạn lý thuyết về kiến thức Định lí Ta-lét trong tam giác. Hy vọng rằng bài viết thực sự hữu ích với bạn. Để có thể có kết quả cao hơn trong học tập, mời bạn hãy ghé thăm các bài viết khác của chúng tôi. Hoặc có nhu cầu tìm gia sư dạy kèm thì hãy liên hệ với giasudiem10 nhé.
