Số thực là gì? Tập số thực và trục số chi tiết

Trong bài viết hôm nay chúng ta cùng tìm hiểu về số thực. Một trong những tập hợp số quan trọng bao gồm kiến thức về số thực, biểu diễn trên trục số, và các bài tập về số thực.

Số thực là gì?

Số thực là tập hợp số bao gồm số nguyên dương (ví dụ 1, 2, 3,…), số 0, số nguyên âm (ví dụ -1, -2, -3,…) số hữu tỉ (ví dụ 5/2, -2/3), số vô tỉ (ví dụ số pi, số √2). Trên trục số số thực biểu diễn mọi điểm trên đó.

Kí hiệu số thực là R. Số thực là tập hợp các số hữu tỉ và số vô tỉ: R = Q ∪ I.

Số thực bao gồm các số thực âm, số 0 và số thực dương.

Một số tập hợp số bao gồm:

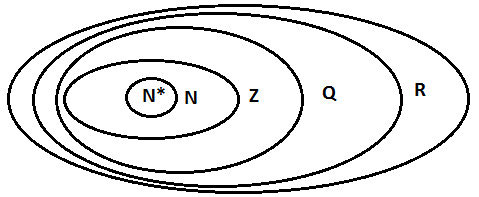
Tập hợp số tự nhiên kí hiệu là N: N = {0, 1, 2, 3,…}
Tập hợp các số nguyên kí hiệu là Z: Z = {…, -3, -2, -1, 0, 1, 2, 3,…}
Tập hợp các số hữu tỉ Q: Q = {x = a/b; a, b ϵ Z, b ≠0}
Tập hợp các số vô tỉ I: I ={các số thập phân vô hạn không có tuần hoàn, ví dụ như √2, số pi}

Các ví dụ về số thực đó là:

Số tự nhiên: 1, 6, 3, 4, 5,…
Số nguyên: −17, -2, 3, 8,…
Số hữu tỉ: 4/3, 7/10,…
Số vô tỉ: √2 = 1,41421356…; pi = 3,1456…,….

Biểu diễn số thực trên trục số

Trên trục số mỗi điểm điều biểu diễn một số thực hay nói đơn giản mọi điểm trên trục số là 1 số thưc. Trên trục số tập hợp số thực bao gồm số nguyên âm, số nguyên dương, số 0, số hữu tỉ, số vô tỉ….

>>Xem thêm: Tổng hợp công thức lũy thừa giải bài tập nhanh.

Một số tập hợp số quen thuộc

Số thực gồm:

Số tự nhiên N: N = {0, 1, 2, 3…}
Số nguyên Z: Z = {…-3, -2, -1, 0, 1, 2, 3…}
Số hữu tỉ Q: Q = {x = a/b; trong đó a,b ϵ Z, và b ≠0}
Số vô tỉ I: I ={thập phân vô hạn không tuần hoàn, ví dụ căn bậc 2}

Một số bài tập về số thực

Ví dụ 1: Điền dấu ∈, ∉, ⊂ thích hợp vào chỗ trống (…):

4 …. Q ; 5 …. R ; 7… I ; -2,53… Q ;

0,2(35) …. I ; N …. Z ; I …. R.

Giải:

a) 4 ∈ Q ; 5 ∈ R ; 7 ∉ I ; -2,53∈ Q ;

b) 0,2(35) ∉ I ; N ∈ Z ; I ⊂ R.

Các bạn thường hay nhầm lẫn quan hệ giữ số và tập hợp là thuộc hay không thuộc. Ví dụ: 4 ∈ Q ; 7 ∉ I

Quan hệ giữa các tập hợp với nhau là ⊂.

Ví dụ 2: Hãy tìm các tập hợp

a) Q ∩ I ;
b) R ∩ I.

Giải.

a) Q ∩ I = Ø ;
b) R ∩ I = I.

>>Xem thêm: Tập hợp là gì? Những tập hợp số quen thuộc.

Bài tập so sánh 2 số thực

Phương pháp giải:

Cần nắm vững những kiến thức dưới đây:

Với hai số thực x, y bất kì thì ta luôn có hoặc x = y hoặc x < y hoặc x > y.
Những số thực lớn hơn 0 gọi là số thực dương, các số thực nhỏ hơn 0 gọi là số thực âm.
Số 0 không là số thực dương cũng không phải là số thực âm.
Việc so sánh số thực dương làm tương tự như so sánh các số hữu tỉ.

Phương pháp giải so sánh về các số thực

Bài tập ví dụ

Ví dụ 1

Điền chữ số thích hợp vào (…) :

a) – 3,02 < – 3, … 1
b) – 7,5 … 8 > – 7,513 ;
c) – 0,4 … 854 < – 0,49826 ;
d) -1, … 0765 < – 1,892.

Hướng dẫn

a) – 3,02 < – 301
b) – 7,508 > – 7,513 ;
c) – 0,49854 < – 0,49826 ;
d) -1,90765 < – 1,892.

Ví dụ 2

Cho các số thực: -3,2 ; 1 ; -1/2 ; -7,4 ; 0 ; -1,5. Hãy sắp xếp:

a) Theo thứ tự từ nhỏ đến lớn.
b) Theo thứ tự từ bé đến lớn theo giá trị tuyệt đối của chúng.

Giải.

a)Sắp xếp theo thứ tự như sau: – 3,2 < -1,5 < -1/2 < 0 < 1 < 7,4.

b) 0 < 1/2 < 1 < 1,5 < 3,2 < 7,4. Vì vậy:

|0| < |-1/2| < |1| < |-1,5| < |-3,2| < |7,4|.

Tìm x trong một đẳng thức

Phương pháp giải

Cần sử dụng đến tính chất của các phép toán
Sử dụng quan hệ giữa những số hạng trong một tổng, một hiệu; quan hệ giữa các thừa số trong một tích, quan hệ giữa số bị chia, số chia và thương ở phép chia.
Sử dụng theo quy tắc “dấu ngoặc”, “chuyển vế”