Việc nhớ hàng trăm công thức Toán lớp 6 không phải là việc đơn giản, vì vậy giasudiem10 đã biên soạn bài Tổng hợp công thức toán lớp 6 đại số và hình học đầy đủ, chi tiết nhất với mục đích giúp các em học sinh dễ nhớ hơn. Loạt bài này sẽ là công thức hướng dẫn giúp bạn học tốt môn Toán lớp 6 hơn.
Mục Lục
1. Đại số
1.1 Các phép tinh cộng, trừ, nhân, chia, nâng lên lũy thừa
|
Phép tính |
Số thứ nhất |
Số thứ hai |
Dấu phép tính |
Kết quả phép tính |
Điều kiện để kết quả là số tự nhiên |
|
Cộng a + b |
Số hạng |
Số hạng |
+ |
Tổng |
Mọi a và b |
|
Trừ a – b |
Số bị trừ |
Số trừ |
– |
Hiệu |
a ≥ b |
|
Nhân a.b hoặc a x b |
Thừa số |
Thừa số |
x , . |
Tích |
Mọi a và b |
|
Chia a : b |
Số bị chia |
Số chia |
: |
Thương |
b ≠ 0, a = b.k, k ∈ N |
|
Nâng lên lũy thừa an |
Cơ số |
Số mũ |
Viết số mũ nhỏ và đưa lên cao |
Lũy thừa |
Mọi a và n, trừ 00 |
1.2 Dấu hiệu chia hết
|
Chia hết cho |
Dấu hiệu |
Chia hết cho |
Dấu hiệu |
|
2 |
Chữ số tận cùng là số chẵn |
5 |
Chữ số tận cùng là 0 hoặc 5 |
|
3 |
Tổng các chữ số chia hết cho 3 |
9 |
Tổng các chữ số chia hết cho 9 |
1.3 Cách tìm ƯCLN và BCNN
|
Tìm ƯCLN |
Tìm BCNN |
|
|
1. |
Phân tích các thừa số nguyên tố. |
|
|
2. |
Chọn các thừa số nguyên tố |
|
|
CHUNG |
CHUNG và RIÊNG |
|
|
3. |
Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ: |
|
|
NHỎ NHÂT |
LỚN NHẤT |
|
1.4 Số nguyên
|
Tính chất của phép cộng các số nguyên |
a + b = b + a |
(a + b) + c = a + (b + c) |
a + 0 = 0 + a = 0 |
a + (-a) = 0 |
|
Phép trừ 2 số nguyên |
a – b = a + (-b) |
|
|
|
|
Nhân 2 số nguyên |
a.0 = 0.a = 0 |
Nếu a,b cùng dấu thì a.b = a . b= |a|.|b| |
Nếu a,b trái dấu thì a.b = – |a| . |b| |
|
|
Tính chất của phép nhân |
a.b = b.a |
(a.b).c = a.(b.c) |
a.1 = 1.a = a |
a (b + c) = a.b + a.c |
|
Bội và ước của số nguyên |
a |
a |
a |
|
b, b1.5 Phân số
|
a = c nếu a.d = b.c b d |
a = a.m b b.m (m ≠0, m ∈ Z ) |
|
a + b = a + b m m m |
a – b = a – b m m m |
1.6 Tính chất của phép cộng và nhân phân số
2. Hình học
2.1 Điểm, ba điểm thẳng hàng
- Đặt tên điểm A, B,C
- 3 điểm thẳng hàng : A ∈ d , B ∈ d , C ∈ d ⇒ A, B,C thẳng hàng
- Trong ba điểm thẳng hàng, có một điểm và chỉ một điểm nằm giữa hai điểm còn lại
- Qua 2 điểm phân biệt ta vẽ được 1 và chỉ 1 đường thẳng.
2.2 Phân biệt đường thẳng – tia – đoạn thẳng
|
|
Đường thẳng |
Tia |
Đoạn thẳng |
|
Hình vẽ |
 |
|
|
|
Số đầu bị giới hạn |
Không |
1 đầu |
2 đầu |
|
Cách đặt tên |
– 1 chữ cái in thường a, b, c,… – 2 chữ cái in thường xy, yx,… – 2 chữ cái in Hoa AB, BA,… ( A, B thuộc đường thẳng) |
(Ưu tiên đọc gốc trước) O ∈ xy ⇒ Ox,Oy |
Nếu A, B là đầu mút ⇒ AB hoặc BA |
|
Qua n điểm không thẳng hàng vẽ được |
n(n -1) đường thẳng 2 |
n(n – 1) tia |
n(n -1) đoạn thẳng 2 |
2.3 Vị trí của 2 đường thẳng
|
Vị trí tương đối |
Số điểm chung |
Hình vẽ |
|||||||
|
Hai đường thẳng trùng nhau |
Vô số |
 |
|||||||
|
Hai đường thẳng song song |
Không có |
 |
|||||||
|
Hai đường thẳng cắt nhau |
1 |
|
|||||||
2.4 Tia
Hình gồm điểm 0 và một phần đường thẳng bị chia ra bởi điểm O được gọi là một tia gốc O
| Đối nhau | Trùng nhau | Phân biệt | |
| Hình vẽ |  |
 |
 |
| Nhận xét |
Chung gốc Tạo thành 1 đường thẳng |
Chung gốc Tạo thành 1 tia | Không trùng nhau |
2.5 Trung điểm của đoạn thẳng
M là trung điểm của AB ⇔ M nằm giữa A và B ; MA = MB hoặc MA = MB = AB
2
2.6 Các cách chứng minh 1 điểm nằm giữa 2 điểm còn lại
– Cách 1: OA,OB đối nhau Þ O nằm giữa A và B
– Cách 2: So sánh độ dài đoạn thẳng chung 1 đầu trên cùng 1 tia Trên cùng 1 tia Ox : OA = a,OB = b(a < b)
Ta có : OA < OB ⇒ A nằm giữa O và B
– Cách 3: AM + MB = AB ⇒ M nằm giữa A và B
– Cách 4: M là trung điểm AB ⇒ M nằm giữa A và B
2.7 Góc – phân loại góc
– Góc xOy là hình gồm 2 tia chung gốc Ox,Oy . Kí hiệu :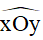 
– Oo < góc nhọn < 90o ( góc vuông ) < góc tù < 180o ( góc bẹt )
– Các cặp góc :
Hai góc kề nhau Hai góc bù nhau
Hai góc phụ nhau Hai góc kề bù
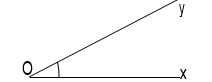
– n tia chung gốc ta vẽ được : n(n -1) góc
2
2.8 Tia nằm giữa hai tia
– Nếu tia Oy nằm giữa hai tia Ox và Oz thì: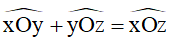 
– Ngược lại nếu thì: tia Oy nằm giữa hai tia Ox,Oz
- Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nửa mặt phẳng đối nhau có bờ chứa cạnh
- Hai góc phụ nhau là hai góc có tổng số đo bằng 90o .
- Hai góc bù nhau là hai góc có tổng số đo bằng 180o .
- Hai góc vừa kề nhau, vừa bù nhau là hai góc kề bù
– Chú ý:
+ Với bất kì số m nào, , trên nửa mặt phẳng có bờ là đường thẳng chứa tia Ox bao giờ cũng vẽ được một và chỉ một tia Oy sao cho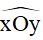 
= (độ).
+ Nếu có các tia Oy, Oz thuộc cùng một nửa mặt phẳng bờ chứa tia Ox và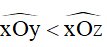 
thì tia Oy nằm giữa hai tia Ox và Oz.
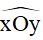+ = m0,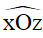 
= n0, vì m0 < n0 nên tia Oy nằm giữa hai tia Ox và Oz.
2.9 Tia phân giác của một góc
Tia phân giác của một góc là tia nằm giữa hai cạnh của góc và tạo với hai cạnh ấy hai góc bằng nhau.
Tia Ot là tia phân giác của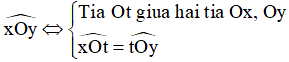 
Hoặc: Tia Ot là tia phân giác của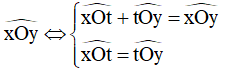 
Hoặc: Tia Ot là tia phân giác của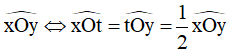 
2.10 Đường tròn
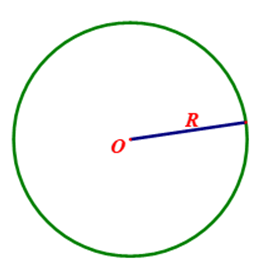
– Đường tròn tâm O, bán kính R là hình gồm các điểm cách O một khoảng bằng R, kí hiệu (O;R).
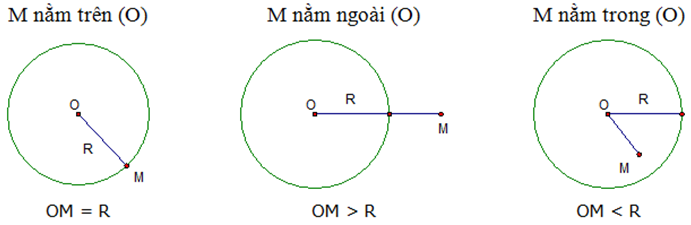
– Với mọi điểm M nằm trong mặt phẳng thì:
+ Nếu OM < R: điểm M nằm trong đường tròn
+ Nếu OM = R: điểm M nằm trên (thuộc) đường tròn.
+ Nếu OM > R: điểm M nằm ngoài đường tròn.
– Hình tròn: là hình gồm các điểm nằm trên đường tròn và các điểm nằm bên trong đường tròn đó.
– Cung, dây cung, đường kính:
+ Hai điểm A, B nằm trên đường tròn chia đường tròn thành hai phần, mỗi phần gọi là một cung tròn (cung). Hai điểm A, B là hai mút của cung.
+ Đoạn thẳng AB gọi là một dây cung.
+ Dây cung đi qua tâm là đường kính (đường kính MN).
– Đường kính dài gấp đôi bán kính và là dây cung lớn nhất.
2.11 Tam giác
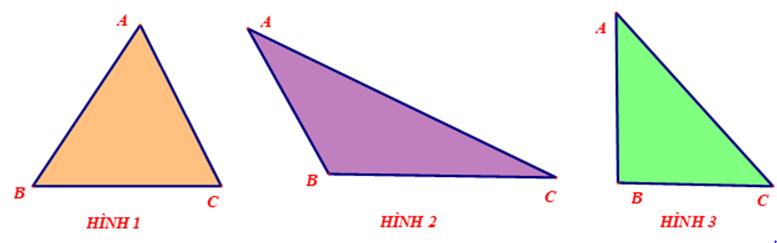
– Tam giác ABC là hình gồm ba đoạn thẳng AB, BC, CA khi ba điểm A, B, C không thẳng hàng. Kí hiệu: ΔABC.
– Một tam giác có: 3 cạnh, 3 đỉnh, 3 góc.
– Một điểm nằm bên trong tam giác nếu nó nằm trong cả 3 góc của tam giác. Một điểm không nằm trong tam giác và không nằm trên cạnh nào của tam giác gọi là điểm ngoài của tam giác.
Tam giác có cả ba góc nhọn gọi là tam giác nhọn (HÌNH 1), có 1 góc tù là tam giác tù (HÌNH 2), có 1 góc vuông là tam giác vuông (HÌNH 3).
