Các em cần nắm rõ kiến thức và các dạng bài tập về số phức khi hiểu rõ vấn đề này chúng ta cùng tìm hiểu một số bài tập đơn giản về số phức. Chúng ta cùng tìm hiểu nhé!
1. Công thức số phức



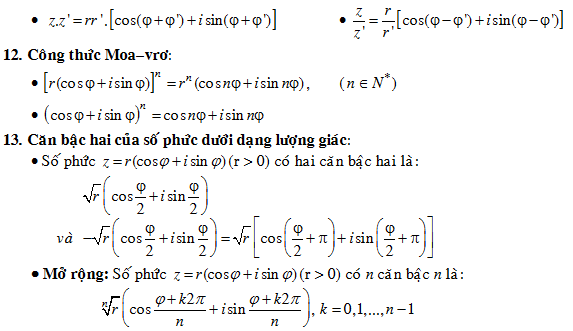
2. Một số bài tập số phức
2.1 Tìm số phức thỏa mãm
Ví dụ 1: Tìm các số thực x, y sao cho đẳng thức sau là đúng:
a) 5x + y + 5xi = 2y – 1 + (x-y)i
b) (-3x + 2y)i + (2x – 3y + 1)=(2x + 6y – 3) + (6x – 2y)i
Hướng dẫn:
a) Ta xem xét mỗi vế là một số phức, như vậy điều kiện để 2 số phức bằng nhau là phần thực bằng phần thực, phần ảo bằng phần ảo.
Ta có: 5x + y = 2y – 1; 5x = x – y, suy ra x = -1/7; y = 4/7
b) Câu này tương tự câu trên, các bạn cứ việc đồng nhất phần thực bằng phần thực, phần ảo bằng phần ảo là sẽ tìm ra được đáp án.
>>Xem thêm: Công thức lượng giác chi tiết.
Ví dụ 2: Tìm số phức biết:
a) |z| = 5 và z = z
b) |z| = 8 và phần thực của z bằng 5 lần phần ảo của z.
Hướng dẫn:
a) Giả sử z = a + bi, suy ra z = a – bi . Khi đó:
a2 + b2 = 52; a = a; b = -b (do z = z)
suy ra b = 0, a = 5
Vậy có 2 số phức z thỏa đề bài là z = 5 và z = -5
b) Hướng đi là lập hệ phương trình bậc nhất hai ẩn, từ đó giải tìm ra được phần thực và phần ảo của z.
Như vậy, cách để giải quyết dạng này là dựa vào các tính chất của số phức, ta lập các hệ phương trình để giải, tìm ra phần thực và ảo của số phức đề bài yêu cầu.
>>Xem thêm: Công thức nguyên hàm đầy đủ.
2.2 Căn bậc 2 và bình phương số phức
Cho số phức z = a + bi, số phức w = x + yi được gọi là căn bậc hai của z nếu w2 = z, hay nói cách khác:
(x + yi)2 = a + bi
=> x2 – y2 + 2xyi = a + bi
=> x2 – y2 = a, 2xy=b(*).
Như vậy để tìm căn bậc 2 của một số phức, ta sẽ giải hệ phương trình (*) ở đã nêu ở trên.
Ví dụ: Tìm giá trị của m để phương trình sau z + mz + i = 0 có hai nghiệm z1 , z2 thỏa đẳng thức z1 2 + z2 2 = -4i.
Hướng dẫn:
Chú ý, đối với phương trình bậc 2 thì hệ thức Vi-et về nghiệm luôn được sử dụng. Như vậy ta có: z1 + z2 = -m, z1z2 = i.
Theo đề bài:
z1 2 + z2 2 = -4i
=> (z1 + z2)2 – 2z1z2 = -4i
=> m2 = -2i.
Đến đây, bài toán qui về tìm căn bậc hai cho 1 số phức. Áp dụng phần kiến thức đã nêu ở trên, ta giải hệ sau: gọi m=a+bi, suy ra ta có hệ:
a2 + b2 = 0, 2ab = -2i
=> (a,b) = (1,-1) hoặc (a,b) = (-1,1).
Vậy có hai giá trị của m thỏa mãn đề bài.
>>Xem thêm: Công thức và bài tập hệ thức Vi et.
2.3 Tìm tập hợp số phức thỏa mãm
Để giải dạng bài tập này, các bạn phải vận dụng một số kiến thức toán 12 hình học giải tích bao gồm phương trình đường thẳng, đường tròn, parabol…, chú ý công thức tính module của số phức, nó sẽ giúp ích rất nhiều cho các bạn khi quỹ tích liên quan đến hình tròn hoặc parabol.
– Số phức z thỏa mãn điều kiện độ dài, chú ý cách tính module: ![]()
– Nếu số phức z là số thực, a=0.
– Nếu số phức z là số thuần ảo, b=0.
Ví dụ: Tìm tập hợp các điểm M thỏa mãn:
a) (2z – i)/(z – 2i) có phần thực là 3.
b) |z – 1 + 2i| = 3
Hướng dẫn:
a) Gọi M(x,y) là điểm cần tìm. Khi đó: (2z – i)/(z – 2i)= a + bi với:
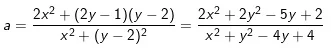
Để phần thực là 3, tức là a=3, suy ra:

Vậy tập hợp các điểm M là đường tròn tâm I(0;17/2) có bán kính: ![]()
b) M(x,y) là điểm biểu diễn của z, gọi N là điểm biểu diễn của số phức z = 1 – 2i,
suy ra N(1,-2).
Theo đề bài, |z – z2|= 3, suy ra MN=3
Vậy tập hợp các điểm M thỏa mãn đề là đường tròn tâm N(1;-2) bán kính R=3.
>>Xem thêm: Số phức nghịch đảo lý thuyết và bài tập.
Chúc các bạn thành công!