Khi giải phương trình lượng giác chúng ta gặp rất nhiều bài toán đưa về dạng phương trình lượng giác đặc biêt như sinx=a,cosx=a,tanx=a,cotx=a. Bài này sẽ giải nghiệm cụ thể trong các trường hợp đặc biệt a=0,a=1,a=−1.
1. Phương trình lượng giác đặc biệt
Nghiệm của phương trình lượng giác đặc biệt sinx=0,1,−1
sinx=0⇔x=k.π,k∈Z
sinx=1⇔x=π2+k.2π,k∈Z
sinx=−1⇔x=−π2+k.2π,k∈Z
Nghiệm của phương trình lượng giác đặc biệt cosx=0,1,−1
cosx=0⇔x=π2+k.π,k∈Z
cosx=1⇔x=k.2π,k∈Z
cosx=−1⇔x=π+k.2π,k∈Z
Nghiệm của phương trình lượng giác đặc biệt tanx=0,1,−1
tanx=0⇔x=k.π,k∈Z
tanx=1⇔x=π4+k.π,k∈Z
tanx=−1⇔x=−π4+k.π,k∈Z
Nghiệm của phương trình lượng giác đặc biệt cotx=0,1,−1
cotx=0⇔x=π2+k.π,k∈Z
cotx=1⇔x=π4+k.π,k∈Z
cotx=−1⇔x=−π4+k.π,k∈Z
>>Xem thêm: Tổng hợp công thức lượng giác đầy đủ.
2. Phương trình lượng giác cơ bản
Phương trình sinx = a
♦ |a| > 1: phương trình (1) vô nghiệm.
♦ |a| ≤ 1: gọi α là một cung thỏa mãn sinα = a.
Khi đó phương trình (1) có các nghiệm là
x = α + k2π, k ∈ Z
và x = π-α + k2π, k ∈ Z.
Nếu α thỏa mãn điều kiện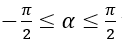 
và sinα = a thì ta viết α = arcsin a.
Khi đó các nghiệm của phương trình (1) là
x = arcsina + k2π, k ∈ Z
và x = π – arcsina + k2π, k ∈ Z.
Phương trình cosx = a
♦ |a| > 1: phương trình (2) vô nghiệm.
♦ |a| ≤ 1: gọi α là một cung thỏa mãn cosα = a.
Khi đó phương trình (2) có các nghiệm là
x = α + k2π, k ∈ Z
và x = -α + k2π, k ∈ Z.
Nếu α thỏa mãn điều kiện 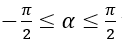và cosα = a thì ta viết α = arccos a.
Khi đó các nghiệm của phương trình (2) là
x = arccosa + k2π, k ∈ Z
và x = -arccosa + k2π, k ∈ Z.
Phương trình tanx = a
Điều kiện: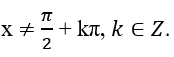 
Nếu α thỏa mãn điều kiện 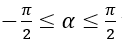và tanα = a thì ta viết α = arctan a.
Khi đó các nghiệm của phương trình (3) là
x = arctana + kπ,k ∈ Z
Phương trình cotx = a
Điều kiện: x ≠ kπ, k ∈ Z.
Nếu α thỏa mãn điều kiện 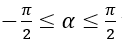và cotα = a thì ta viết α = arccot a.
Khi đó các nghiệm của phương trình (4) là
x = arccota + kπ, k ∈ Z
Chúc các bạn thành công!
