Nhằm tạo một môi trường học tập dành cho các em. Bài học tiếp theo hôm nay chúng ta sẽ tiếp tục về định nghĩa và tính chất về trục đối xứng. Chúng ta cùng nắm rõ kiến thức để làm bài tập và áp dụng thật tốt nhé.
1. Định nghĩa trục đối xứng
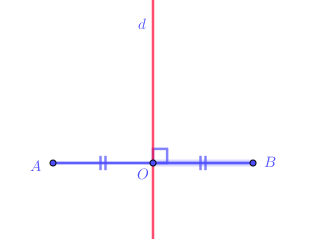
Chú Ý: Nếu điểm M nằm trên đường thẳng d thì điểm đối xứng với M qua đường thẳng d cũng là điểm M .
2. Hình đối xứng qua trục
Định nghĩa: Hai hình gọi là đối xứng với nhau qua đường thẳng a nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng a và ngược lại. Đường thẳng a gọi là trục đối xứng của hai hình đó.
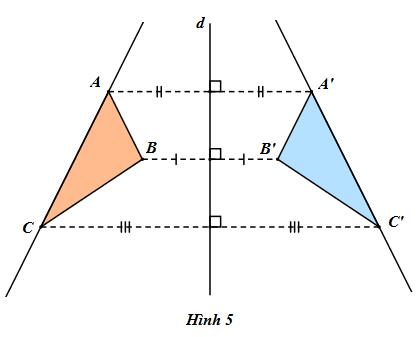
Chú ý: Nếu hai hình đối xứng nhau qua trục thì chúng bằng nhau.
>>Xem thêm: Kiến thức về tia phân giác.
3. Hình có trục đối xứng
Đường thẳng d gọi là trục đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng thuộc hình H . Ta nói hình H có trục đối xứng.
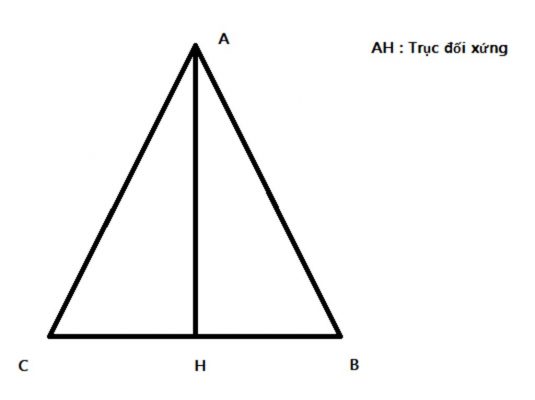
Định lý: Trục đối xứng của hình thang cân là đường thẳng đi qua trung điểm hai cạnh đáy của hình đó.
4. Một số bài tập trục đối xứng
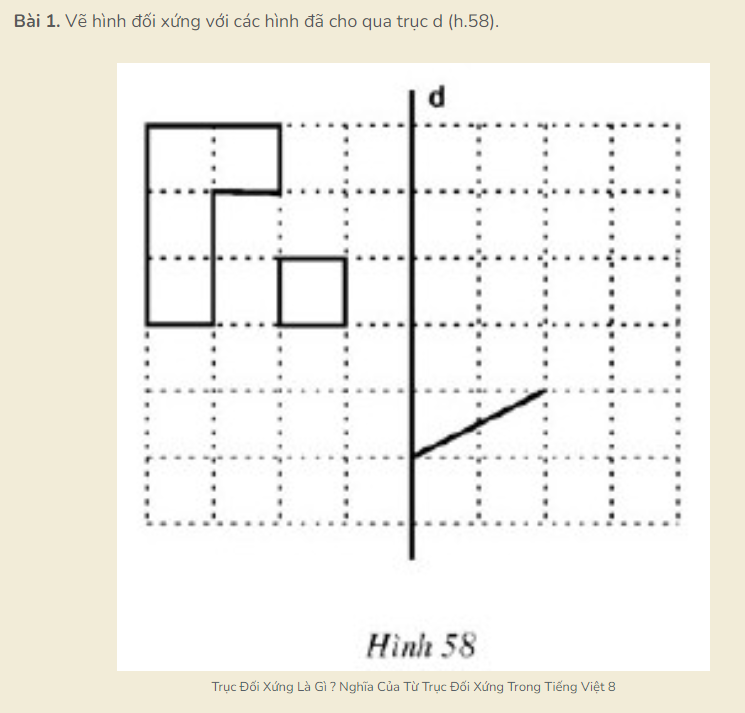

Chúc các bạn thành công!
Nhằm tạo một môi trường học tập dành cho các em. Bài học tiếp theo hôm nay chúng ta sẽ tiếp tục về định nghĩa và tính chất về trục đối xứng. Chúng ta cùng nắm rõ kiến thức để làm bài tập và áp dụng thật tốt nhé.
1. Định nghĩa trục đối xứng

Chú Ý: Nếu điểm M nằm trên đường thẳng d thì điểm đối xứng với M qua đường thẳng d cũng là điểm M .
2. Hình đối xứng qua trục
Định nghĩa: Hai hình gọi là đối xứng với nhau qua đường thẳng a nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng a và ngược lại. Đường thẳng a gọi là trục đối xứng của hai hình đó.

Chú ý: Nếu hai hình đối xứng nhau qua trục thì chúng bằng nhau.
>>Xem thêm: Kiến thức về tia phân giác.
3. Hình có trục đối xứng
Đường thẳng d gọi là trục đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng thuộc hình H . Ta nói hình H có trục đối xứng.

Định lý: Trục đối xứng của hình thang cân là đường thẳng đi qua trung điểm hai cạnh đáy của hình đó.
4. Một số bài tập trục đối xứng


Chúc các bạn thành công!
Nhằm tạo một môi trường học tập dành cho các em. Bài học tiếp theo hôm nay chúng ta sẽ tiếp tục về định nghĩa và tính chất về trục đối xứng. Chúng ta cùng nắm rõ kiến thức để làm bài tập và áp dụng thật tốt nhé.
1. Định nghĩa trục đối xứng

Chú Ý: Nếu điểm M nằm trên đường thẳng d thì điểm đối xứng với M qua đường thẳng d cũng là điểm M .
2. Hình đối xứng qua trục
Định nghĩa: Hai hình gọi là đối xứng với nhau qua đường thẳng a nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng a và ngược lại. Đường thẳng a gọi là trục đối xứng của hai hình đó.

Chú ý: Nếu hai hình đối xứng nhau qua trục thì chúng bằng nhau.
>>Xem thêm: Kiến thức về tia phân giác.
3. Hình có trục đối xứng
Đường thẳng d gọi là trục đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng thuộc hình H . Ta nói hình H có trục đối xứng.

Định lý: Trục đối xứng của hình thang cân là đường thẳng đi qua trung điểm hai cạnh đáy của hình đó.
4. Một số bài tập trục đối xứng


Chúc các bạn thành công!
Nhằm tạo một môi trường học tập dành cho các em. Bài học tiếp theo hôm nay chúng ta sẽ tiếp tục về định nghĩa và tính chất về trục đối xứng. Chúng ta cùng nắm rõ kiến thức để làm bài tập và áp dụng thật tốt nhé.
1. Định nghĩa trục đối xứng

Chú Ý: Nếu điểm M nằm trên đường thẳng d thì điểm đối xứng với M qua đường thẳng d cũng là điểm M .
2. Hình đối xứng qua trục
Định nghĩa: Hai hình gọi là đối xứng với nhau qua đường thẳng a nếu mỗi điểm thuộc hình này đối xứng với một điểm thuộc hình kia qua đường thẳng a và ngược lại. Đường thẳng a gọi là trục đối xứng của hai hình đó.

Chú ý: Nếu hai hình đối xứng nhau qua trục thì chúng bằng nhau.
>>Xem thêm: Kiến thức về tia phân giác.
3. Hình có trục đối xứng
Đường thẳng d gọi là trục đối xứng của hình H nếu điểm đối xứng với mỗi điểm thuộc hình H qua đường thẳng d cũng thuộc hình H . Ta nói hình H có trục đối xứng.

Định lý: Trục đối xứng của hình thang cân là đường thẳng đi qua trung điểm hai cạnh đáy của hình đó.
4. Một số bài tập trục đối xứng


Chúc các bạn thành công!




















