TAM GIÁC VUÔNG BẰNG NHAU

TAM GIÁC VUÔNG BẰNG NHAU

I. Các kiến thức cần nhớ

1. Nhắc lại các trường hợp bằng nhau đã biết

+ Nếu hai cạnh góc vuông của tam giác vuôngnày lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằngnhau (cạnh-góc-cạnh).

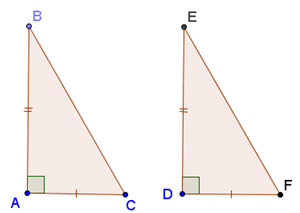
+ Nếu một cạnh góc vuông và một góc nhọn kềcạnh ấy của tam giác vuông này bằng một cạnhgóc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằngnhau (góc-cạnh-góc).

+ Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một gócnhọn của tam giác vuông kia thì hai tam giácvuông đó bằng nhau (cạnh huyền – góc nhọn)

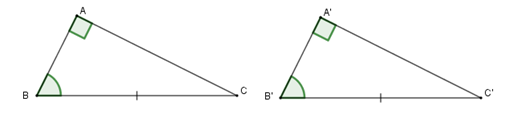
2. Trường hợp bằng nhau cạnh huyền vàcạnh góc vuông

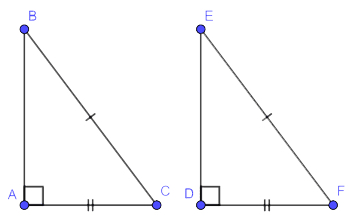
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnhgóc vuông của tam giác vuông kia thì hai tam giác đó bằng nhau.

Ví dụ:

==90°

BC=B′C′          

AC=A′C′

⇒ΔABC=ΔA′B′C′(cạnh huyền– cạnh gócvuông)

II. Các trường hợp bằng nhau của tam giác vuông

*Hai cạnh góc vuông:

–Nếu hai cạnh góc vuông của tam giác vuôngnày lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằngnhau (cạnh – góc – cạnh )

*Cạnh góc vuông và góc nhọn kề cạnh đó

–Nếu một cạnh góc vuông và một góc nhọn kềcạnh ấy của tam giác vuông này bằng một cạnhgóc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằngnhau ( góc – cạnh – góc )

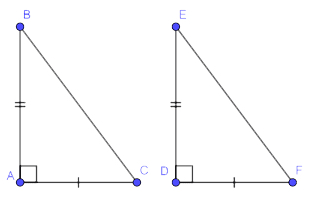
*Cạnh huyền – góc nhọn 

– Nếu cạnh huyền và một góc nhọn của tam giácvuông này bằng cạnh huyền và một góc nhọncủa tam giác vuông kia thì hai tam giác vuôngđó bằng nhau ( góc – cạnh – góc)

*Cạnh huyền – cạnh góc vuông

– Nếu cạnh huyền và một cạnh góc vuông củatam giác vuông này bằng cạnh huyền và mộtcạnh góc vuông của tam giác vuông kia thì haitam giác vuông đó bằng nhau.

Muốn chứng minh hai đoạn thẳng[hay hai góc] bằng nhau ta thường làm theo các bước sau:

– Xét xem hai đoạn thẳng[hay hai góc] là hai cạnh [hay hai góc] thuộc hai tam giác nào.

– Chứng minh hai tam giác đó bằng nhau

– Suy ra hai cạnh [hay hai góc] tương ứng bằng nhau.

*. Để tạo ra được hai tam giác bằng nhau, có thể ta phải vẽ thêm đường phụ bằng nhiều cách:

– Nối hai cạnh có sẵn trên hình để tạo ra một cạnh chung của hai tam giác.

– Trên một tia cho trước, đặt một đoạn bằng một đoạn thẳng khác.

– Từ một điểm cho trước, vẽ một đường thẳng song song với một đoạn thẳng.

– Từ một điểm cho trước, vẽ một đường thẳng vuông góc với một đoạn thẳng.

Ngoài ra còn nhiều cách khác ta có thể tích luỹ được kinh nghiệm khi giải nhiều bài toán khác nhau.

Ví dụ minh họa các trường hợp bằng nhaucủa tam giác vuông  

Ví dụ 1:  Cho ΔABC cân ở A ( < 90o). Vẽ BH ⊥AC (H ∈ AC), CK ⊥ AB (K ∈ AB).

a) Chứng minh rằng AH = HK

b) Gọi I là giao điểm của BH và CK. Chứngminh rằng AI là tia phân giác của góc A

   Trả lời: Vẽ hình minh họa:

a) ΔABC cân tại A (giả thiết)

Suy ra  

AB = AC (tính chất)

= (định lí)

Xét hai tam giác vuông HAB và KAC, ta có:  

AB = AC (chứng minh trên)

chung  

⇒ ΔHAB = ΔKAC (cạnh huyền – góc nhọn)

⇒ AH = AK (cặp cạnh tương ứng)

b) Xét hai tam giác vuông KAI và HAI, ta có:

AH = AK (chứng minh trên)

AI cạnh chung

⇒ ΔHAI = ΔKAI (cạnh huyền – cạnh gócvuông)

 =(cặp góc tương ứng)

Hay AI là tia phân giác của

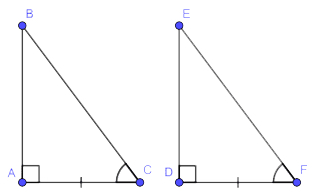
Ví dụ 2: Các tam giác vuông ABC và DEF có   = = 90°, AC = DF. Hãy bổ sung thêm một điềukiện bằng nhau để ΔABC = ΔDEF.  

Trả lời:

+ Bổ sung AB =DE thì ΔABC = ΔDEF (cạnh – góc – cạnh)

+ Bổ sung= thì ΔABC = ΔDEF (góc – cạnh – góc)

+ Bổ sung BC = EF thì ΔABC = ΔDEF (cạnhhuyền – cạnh góc vuông)

Ví dụ 3: Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC.

  Chứng minh rằng:

a) HB = HC

b) =

Trả lời:

a) Xét hai tam giác vuông ΔABH và ΔACH có:

AB = AC (giả thiết)

AH cạnh chung

⇒ ΔABH = ΔACH (cạnh huyền – cạnh gócvuông)

Suy ra HB = HC (cặp cạnh tương ứng)

b) Ta có ΔABH = ΔACH (chứng minh trên)