Trực tâm là một khái niệm quen thuộc trong môn Toán học. Tuy nhiên, có nhiều bạn vẫn hiểu sai về trực tâm. Trong bài viết này, giasudiem10 sẽ giúp bạn hiểu chi tiết “trực tâm là gì?” và các thông tin về tính chất, cách xác định trực tâm của tam giác.
Trực tâm là gì?
Khái niệm: Trực tâm của tam giác là giao điểm 3 đường cao của tam giác. Đường cao của tam giác là đường thẳng đi từ một đỉnh và vuông góc với cạnh đối diện. Một tam giác sẽ có 3 đường cao tương ứng với 3 đỉnh.
Như vậy, 3 đường cao của một tam giác sẽ giao nhau tại 1 điểm gọi là trực tâm. Trực tâm của tam giác có thể nằm bên trong hoặc bên ngoài của tam giác đó, cụ thể là:
- Nếu tam giác có 3 góc nhọn (nhỏ hơn 90 độ) thì trực tâm sẽ nằm trong tam giác.
- Nếu tam giác có 1 góc tù (lớn hơn 90 độ) thì trực tâm sẽ nằm bên ngoài tam giác.
Trực tâm của một số tam giác đặc biệt:
- Trực tâm của tam giác vuông chính là đỉnh góc vuông.
- Trực tâm của tam giác đều cũng chính là trọng tâm, tâm của đường tròn nội ngoại tiếp của tam giác đó. Hay nói cách khác, trực tâm của tam giác đều cách đều 3 đỉnh và 3 cạnh của tam giác đó.
Ví dụ về trực tâm:
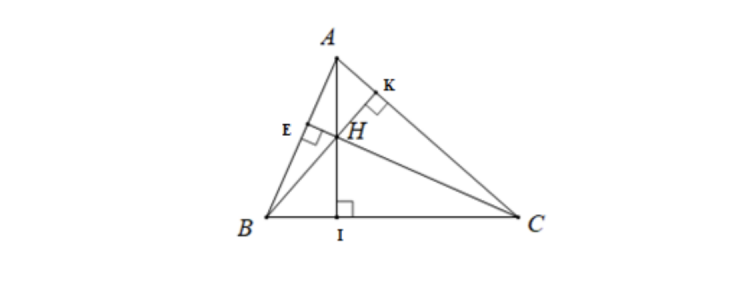
Trong tam giác ABC có 3 đường cao là AI, BK, CE giao nhau tại điểm H. H được gọi là trực tâm của tam giác ABC. Hình minh họa bên dưới.
Các tính chất của trực tâm trong tam giác
Trực tâm của tam giác có những tính chất sau:
- Khoảng cách từ tâm đường tròn ngoại tiếp tam giác đến trung điểm của một cạnh bằng 1/2 khoảng cách từ trực tâm tới đỉnh còn lại của tam giác đó.
- Trong tam giác cân, đường trung trực tương ứng với cạnh đáy cũng chính là đường cao, đường phân giác và đường trung tuyến của tam giác đó.
- Trong một tam giác, nếu đường trung tuyến đồng thời là đường phân giác hoặc đường cao hoặc đường trung trực thì tam giác đó là tam giác cân.
- Trực tâm của tam giác nhọn ABC (có 3 góc nhỏ hơn 90 độ) trùng với tâm đường tròn nội tiếp tam giác được tạo bởi 3 đỉnh là 3 chân đường cao tương ứng với 3 đỉnh của tam giác ABC.
- Đường cao của một đỉnh của tam giác cắt đường tròn ngoại tiếp tam giác ở đâu thì điểm đó là điểm đối xứng với trực tâm của tam giác đó qua cạnh đáy tương ứng với đỉnh. (Định lý Carnot)
Việc nắm vững các tính chất của trực tâm sẽ giúp bạn dễ dàng giải được các bài toán hình học. Vì vậy, bạn hãy cố gắng ghi nhớ các tính chất bên trên nhé.
Cách xác định trực tâm của tam giác
Cách để xác định trực tâm của tam giác thì bạn vẽ 3 đường cao của tam giác đó. Tuy nhiên, trên thực tế, bạn chỉ cần vẽ 2 trong 3 đường cao, giao điểm của chúng ở đâu chính là trực tâm của tam giác đó.
Bạn cũng nên nhớ một số điểm sau để kiểm tra xem mình đã xác định đúng trực tâm của tam giác hay không:
- Trực tâm của tam giác vuông chính là đỉnh của góc vuông.
- Trực tâm của tam giác có 3 góc nhọn nằm bên trong tam giác.
- Trực tâm của tam giác có 1 góc tù nằm bên ngoài tam giác.
Ngoài ra, còn có nhiều cách để xác định trực tâm của tam giác tùy theo từng bài toán cụ thể.
Bài tập về trực tâm tam giác
Để nắm vững hơn kiến thức về trực tâm, bạn có thể tham khảo một số bài tập vận dụng dưới đây.
Bài 1. Cho tam giác ΔABC cân tại A, hai đường cao BD và CE cắt nhau tại I. Tia AI cắt BC tại M. Khi đó ΔMED là tam giác gì?
A. Tam giác cân
B. Tam giác vuông
C. Tam giác vuông cân
D. Tam giác đều.
Đáp án: A
Câu 2: Cho đoạn thẳng AB và điểm M trên cạnh AB (MA < MB). Vẽ tia Mx vuông góc với AB. Trên tia Mx lấy hai điểm C và D sao cho MA = MC, MD = MB. Tia AC cắt BD tại E. Số đo góc DEC là bao nhiêu?
A. 30 độ
B. 45 độ
C. 60 độ
D. 90 độ
Đáp án: D
Bài 3: Cho ΔABC có AC > AB. Trên cạnh AC lấy điểm E sao cho CE = AB. Các đường trung trực của BE và AC cắt nhau tại O. Đáp án nào sau đây đúng?
A. ΔABO = ΔCOE
B. ΔBOA = ΔCOE
C. ΔAOB = ΔCOE
D. ΔABO = ΔCEO
Đáp án C
Lời giải:
Xét tam giác ΔAOB và ΔCOE có
OA = OC (vì O thuộc đường trung trực của AC )
OB = OE (vì O thuộc đường trung trực của BE )
AB = CE (giả thiết)
Do đó ΔAOB = ΔCOE (cạnh – cạnh – cạnh)
Bài 4. Hãy giải thích vì sao trực tâm của tam giác vuông là đỉnh góc vuông và trực tâm của tam giác tù nằm ở bên ngoài tam giác.
Lời giải
Xét ΔABC vuông tại A, ta có:
Vì AB ⏊ AC ⇒ AC là đường cao ứng với cạnh AB và AB là đường cao ứng với cạnh AC
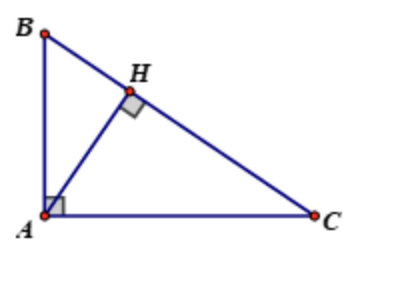
Tức là AB, AC chính là hai đường cao của tam giác ABC cắt nhau tại A
A là trực tâm của tam giác vuông ABC.
Vậy trực tâm của tam giác vuông trùng với đỉnh góc vuông
Xét tam giác tù ABC có A là góc tù.
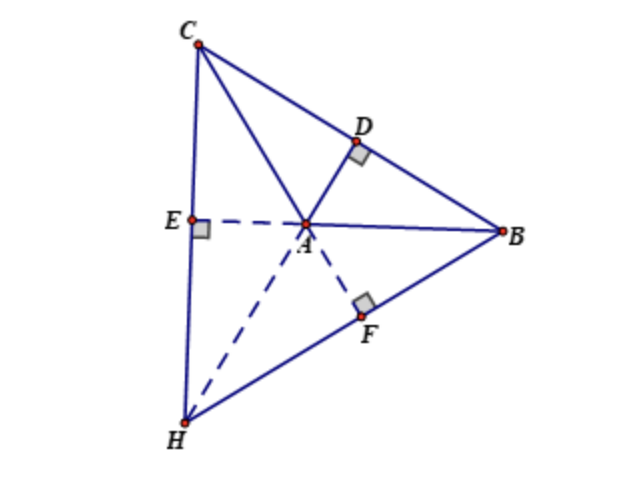
Vẽ các đường cao CE, BF (E thuộc AB, F thuộc AC), trực tâm H.
Giả sử E nằm giữa A và B, khi đó góc BEC lớn hơn góc A và lớn hơn 90 độ
Vậy E nằm ngoài A và B nên tia CE nằm ngoài tia tam giác ABC
Tương tự, tia BF nằm bên ngoài ΔABC.
H là giao của 2 đường cao BF và CE ⇒ trực tâm H nằm bên ngoài ΔABC.
Vậy trực tâm của tam giác tù nằm ở bên ngoài tam giác.
Bài 5: Cho hình vẽ
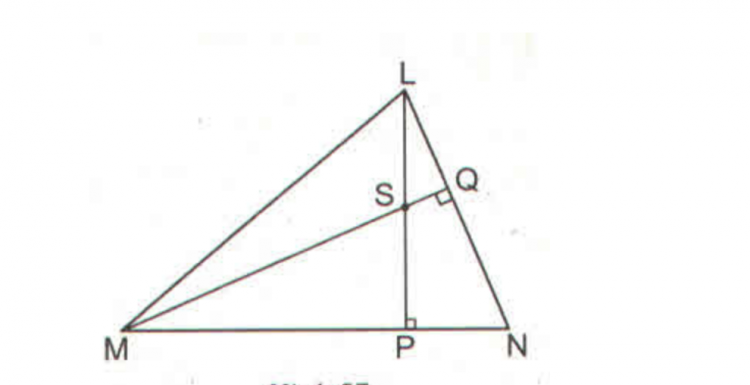
a) Chứng minh S là trực tâm của tam giác MNL
b) Khi góc LNP = 50 độ, hãy tính góc MSP và góc PSQ.
Lời giải:
a)
Xét tam giác MNL có:
MQ ⏊ NL
LP ⏊ MN
Vậy MQ và LP là 2 đường cao của tam giác MNL
Mà MQ và LP cắt nhau tại S nên S là trực tâm của tam giác MNL
b)
Trong tam giác vuông, hai góc nhọn phụ nhau
Xét ΔNMQ vuông tại Q có:
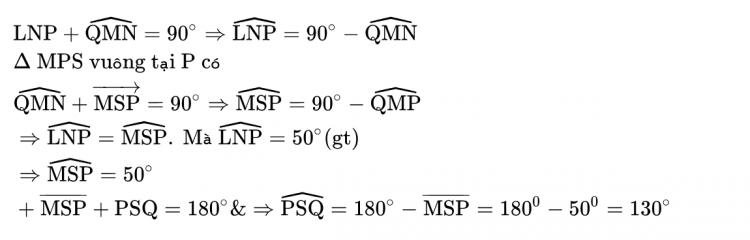
Vậy góc MSP = 50 độ, góc PSQ = 130 độ.
Trên đây là những thông tin về khái niệm trực tâm là gì và các tính chất, cách xác định trực tâm của một tam giác. Hy vọng, qua bài viết sẽ giúp bạn hiểu rõ hơn về khái niệm trực tâm của tam giác.