Định lý cosin, định lý sin trong tam giác là phần kiến thức quan trọng để các em có thể giải nhiều loại bài tập Toán học. Vậy 2 định lý này nói về điều gì và công thức ra sao? Hãy cùng tìm hiểu trong nội dung bài viết dưới đây nhé.
Định lý cosin trong tam giác
Xét tam giác ABC có:
- Độ dài cạnh BC = a
- Độ dài cạnh AC = b
- Độ dài cạnh AB = c
- Các góc A, B, C
- Chu vi tam giác là p
- Bán kính đường tròn nội tiếp là r
- Bán kính đường tròn ngoại tiếp là R
Ta có công thức của định lý cosin như sau:
a2 = b2 + c2 – 2bc.cosA
b2 = a2 + c2 – 2ac.cosB
c2 = a2 + b2 – 2ac.cosC
Suy ra, hệ quả của định lý cosin trong tam giác là:
cosA = (b2 + c2 – a2)/2bc
cosB = (a2 + c2 – b2)/2ac
cosC = (a2 + b2 – c2)/2ab
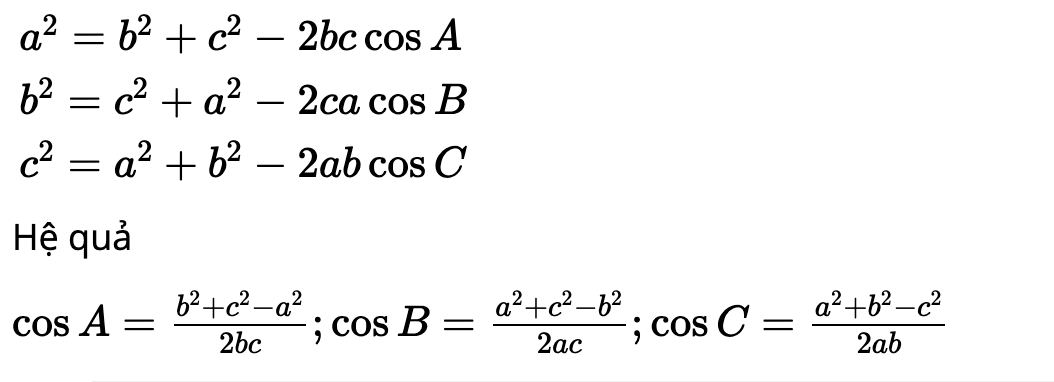
Định lý sin trong tam giác
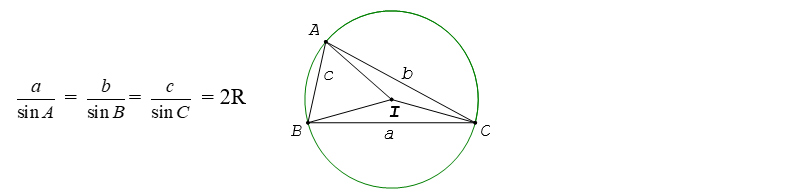
Xét tam giác ABC như trên, ta có công thức của định lý sin như sau:
a/sinA = b/sinB = c/sinC = 2R
Hệ quả của định lý sin trong tam giác:
a = 2R.sinA
b = 2R.sinB
c = 2R.sinC
Công thức tính đường trung tuyến trong tam giác
Gọi ma, mb, mc là độ dài các đường trung tuyến kẻ từ đỉnh A, B, C của tam giác ABC. Ta có công thức tính độ dài các đường trung tuyến trong tam giác ABC như sau:
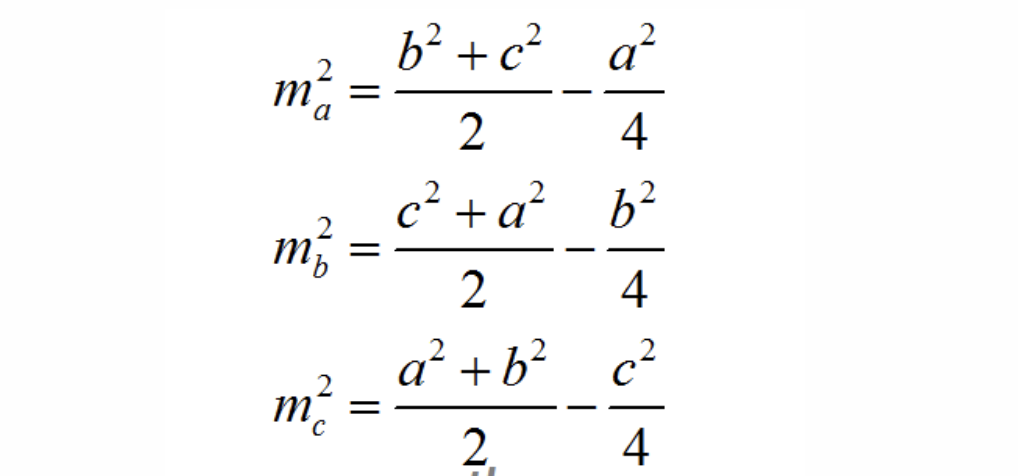
Các công thức tính diện tích tam giác
Gọi ha, hb, hc là độ dài các đường cao kẻ từ đỉnh A, B, C của tam giác ABC. Ta có công thức tính diện tích tam giác ABC như sau:

Bài tập về định lý cosin, định lý sin trong tam giác
Bài 1: Cho tam giác ABC có góc A = 60 độ, AB = 6cm, AC = 8cm. Tính độ dài cạnh BC
Lời giải:
Áp dụng định lý cosin trong tam giác ta có:
BC2 = AB2 + AC2 – 2AB.AC.cosA
BC2 = 62 + 82 – 2.6.8.cos60
BC2 = 36 + 64 – 48 = 52
⇒ BC = 52 = 213
Bài 2: Cho tam giác ABC có cách cạnh BC = 6, AC = 4√2, AB = 2. Tính giá trị cosA và góc A.
Lời giải:
Áp dụng công thức hệ quả của định lý cosin ta có:
cosA = (b2 + c2 – a2)/2bc
cosA = (22 + (4√2)2 – 62)/2.2.4√2 = 0
⇒ A = 90 độ
Trên đây là các công thức của định lý cosin, định lý sin và cách tính diện tích tam giác. Mong rằng, bài viết sẽ giúp các em nắm vững hơn phần kiến thức này và áp dụng hiệu quả trong giải các bài tập.