Bài đăng của giasudiem10 sẽ dạy bạn mọi thứ bạn cần biết về hàm bậc nhất. Ngoài ra còn có các dạng đề thường gặp trong các kỳ thi, đặc biệt là kỳ thi THPT Quốc gia hàng năm.
1. Định nghĩa hàm số bậc nhất
Hàm số được cho bởi công thức y = ax + b với a,b là các số cho trước và a≠0 thì được gọi là hàm số bậc nhất. Và nếu b = 0 thì hàm số bậc nhất có dạng là y = ax, biểu thị tỉ lệ thuận tương quan giữa y và x.
2. Tính biến thiên ở hàm số bậc nhất.
– Ta xét hàm số có dạng y=ax=b (a≠0):
– Tập xác định: D=R
– Khi a>0 thì hàm số đồng biến. Và ngược lại, hàm số nghịch biến khi a<0
– Ta có bảng biến thiên hàm số như dưới đây:
3. Đồ thị hàm số
Hàm số y=ax+b (a#0) là hàm số có đồ thị là một đường thẳng với:
– Hệ số góc là a.
– Hàm số cắt trục hoành tại A(-b/a;0).
– Và cắt trục tung tại B(0;b)
Đặc biệt, trong trường hợp a=0, hàm số sẽ có dạng y=b và là một hàm hằng, có đồ thị là đường thẳng song song với trục hoành.
Lưu ý rằng: khi cho 1 đường thẳng là d có hệ số góc a, đi qua điểm (x0;y0) nó sẽ có phương trình là:
![]()
>>Xem thêm: Mặt phẳng tọa độ là gì? và các dạng bài tập
4. Các dạng toán về hàm số bậc nhất thường gặp
Dạng 1: Tìm hàm số bậc nhất, xét sự tương giao giữa các đồ thị hàm số bậc nhất.
Phương pháp:
Ta sử dụng các bước sau để giải quyết vấn đề xác định hàm bậc nhất:
– Hàm tìm được viết dưới dạng y = ax + b ().
– Lập phương trình thể hiện mối quan hệ giữa a và b bằng cách sử dụng giả thuyết được cung cấp.
– Ta sẽ tìm được hàm số cần tìm khi giải hệ phương trình vừa thiết lập đó
Đối với bài toán tương giao của hai đồ thị bậc nhất ta dùng công thức sau: Gọi đường thẳng d: y = ax + b (a#0), đường thẳng d ‘: y = a’x + b’ (a’#0), ta được nhận xét:
+ d trùng d’ khi và chỉ khi:
![]()
+ d song song d’ khi:
![]()
+ d cắt d’ khi a≠a’, lúc này tọa độ giao điểm chính là nghiệm của hệ phương trình:
![]()
đặc biệt rằng khi ![]() thì đường thẳng d sẽ vuông góc với đường thẳng d’.
thì đường thẳng d sẽ vuông góc với đường thẳng d’.
Ví dụ 1: Hãy xác định hàm số khi xét hàm số bậc nhất có đồ thị là đường thẳng d, biết rằng:
a) d đi qua điểm (1,3) và (2; -1).
b) d song song với d’: 3x-2y + 1 = 0 và đi qua điểm (3; -2).
c) d đi qua điểm (1,2) và cắt tia Ox, Oy lần lượt tại M và N thỏa mãn diện tích tam giác OMN nhỏ nhất.
d) d vuông góc với d’: y = 4x + 3 và đi qua (2; -1).
Gợi ý giải:
Ta có hàm số có dạng y=ax+b (![]() )
)
a) Lưu ý rằng nếu một đường thẳng có dạng y = ax + b (với a#0) khi đi qua điểm (x0; y0) thì sẽ tìm được đẳng thức như sau: y0 = ax0 + b
Ta có hệ phương trình do hàm số đi qua hai điểm (1; 3) và (2; -1).
![]()
⇒ đáp số là ![]() .
.
b) Ta dựa vào tính chất của hai đường thẳng song song và biến đổi đường thẳng d’ về dạng:
![]()
Vì d song song d’, nên suy ra:

Mặt khác d đi qua (3;-2) ⇒ ![]() , suy ra:
, suy ra:

Từ đó ta thu được hàm số cần phải tìm.
>>Xem thêm: Công thức nguyên hàm chi tiết nhất.
c) Tọa độ các điểm cắt lần lượt là:
![]()
Vì giao điểm nằm trên tia Ox và tia Oy nên a<0 và b>0
Nên diện tích tam giác sẽ được tính theo công thức:
![]()
Theo đề bài đã cho, đồ thị đi qua điểm (1;2) ⇒ 2=a+b ⇒ b=2-a
Thay vào công thức để tính diện tích:
⇒ diện tích tam giác MNO sẽ nhỏ nhất khi:

Đáp số cần tìm: ![]()
Lưu ý: Ta sẽ sử dụng bất đẳng thức Cauchy cho 2 số thực dương để giải bài toán trên. Cụ thể rằng: cho hai số thực dương a,b, thì khi đó ta có bất đẳng thức:
![]()
điều kiện bằng xảy ra khi và chỉ khi: a=
d. Do đồ thị đi qua điểm (2;-1) nên: ![]()
Mặt khác ta có d vuông góc d’:
![]()
⇒ ta thu được:
![]()
Ví dụ 2: Cho trước hai đường thẳng d:y=x+2m và d’:y=3x+2.
- Hãy tính vị trí tương đối giữa của hai đường thẳng vừa cho ở trên
- Hãy xác định giá trị tham số m để ta được 3 đường thẳng d, d’ và d’’ đồng quy, biết rằng:
![]()
Gợi ý giải:
a) d và d’ là hai đường thẳng cắt nhau vì 1≠3 (hai hệ số góc khác nhau)
Tọa độ giao điểm của hai đường thẳng là nghiệm của hệ phương trình:
![]()
Vậy tọa độ giao điểm là M(m-1;3m-1)
b) Vì theo đề bài 3 đường thẳng d, d’ và d’’ đồng quy, vậy M ∈d’’. Suy ra:
![]()
Ta có:
m=1, khi đó 3 đường thằng là d:y=x+2; d’: y=3x=2 và d’’: y=-x+2 phân biệt cắt nhau tại giao điểm là (0;2)
m=-3 khi đó d’ trùng với đường thẳng d’’ =>không thỏa mãn tính phân biệt.
Vậy m=1 là chính là đáp số cần tìm.
Dạng 2: Khảo sát biến thiên và vẽ đồ thị hàm số.
Phương pháp: Ta dựa vào tính chất biến thiên đã được nêu ở mục I để giải bài toán này.
Ví dụ 1: Cho hàm số dưới đây, hãy xét sự biến thiên của các hàm số
- y=3x+6
- x+2y-3=0
Gợi ý giải:
a) Tập xác định D=R
a=3>0, suy ra hàm số đã cho đồng biến trên R.
Ta có bảng biến thiên được vẽ như sau:
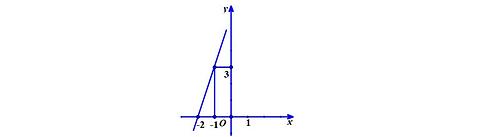
Vẽ đồ thị hàm số: để có thể vẽ đồ thị, ta sẽ xác định các điểm đặc biệt mà đồ thị đi qua. Cụ thể là hai điểm (-2;0) và (-1;3) như hình dưới đây.
b. Biến đổi hàm số về dạng:
![]()
Tập xác định D=R.
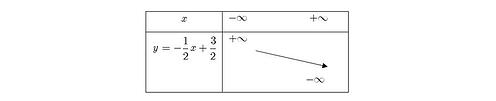
Hệ số góc a<0, suy ra hàm số nghịch biến trên R.
Bảng biến thiên được như sau:
Vẽ đồ thị hàm số:
>>Xem thêm: 7 hằng đẳng thức đáng nhớ.
Dạng 3: Hàm số bậc nhất chứa dấu giá trị tuyệt đối.
Phương pháp: Biểu đồ số có một hình dạng cụ thể và chúng ta có thể vẽ nó theo nhiều cách khác nhau:
Cách 1: Lập đồ thị (C1) cho hàm số y = ax + b có tọa độ thỏa mãn ax+b≥0. Tiếp đó vẽ đồ thị (C2) của hàm số y = -ax-b tại các vị trí x thỏa mãn ax+b<0. Đồ thị © cần phải tìm là hợp của đồ thị (C1) và (C2).
Cách 2: Vẽ đồ thị (C ‘) của hàm số y = ax + b, lấy đối xứng phần đồ thị (C’) bên dưới trục hoành. Sau đó xóa toàn bộ phần đồ thị nằm bên dưới trục hoành. Đồ thị © cần tìm chính là đồ thị còn lại.
Mở rộng:
Cho trước đồ thị hàm số (C) : y=f(x). Khi đó:
- Để vẽ đồ thị (C ‘) của y = f (| x |), chúng ta thực hiện như sau:
Giữ nguyên vị trí của đồ thị (C) bên phải trục tung.
Xóa phần đồ thị bên trái trục tung đối xứng qua trục tung.
-
Chúng ta thực hiện như sau để vẽ đồ thị (C2) của hàm y = | f (x) |:
Giữ nguyên vị trí của đồ thị phía trên trục hoành.
Phần của biểu đồ bên dưới trục hoành đối xứng qua trục hoành, sau đó phần bên dưới trục hoành sẽ xóa đi
Ví dụ: Hãy vẽ đồ thị:
Hướng dẫn:
a. Khi x≥0 thì hàm số có dạng y=2x. Đồ thị hàm số là phần đường thẳng đi qua 2 điểm (0;0) và (1;2) (chú ý rằng chỉ lấy phần bên phải của đường thẳng x=0)
– Khi x<0 thì hàm số có dạng y=-x. Đồ thị là phần đường thẳng đi qua 2 điểm (-1;1) và (-2;2) (chú ý rằng lấy phần đồ thị nằm bên trái đường thẳng x=0)

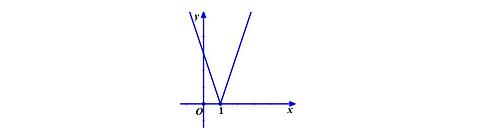
b. Ta vẽ 2 đường thẳng là đường thẳng y=-3x+3 và đường thẳng y=3x-3. Sau đó hãy xóa phần đồ thị nằm dưới trục hoành, lúc này ta sẽ thu được đồ thị cần tìm.
Trên đây là các kiến thức tổng hợp về các phương pháp cơ bản nhất để giải các hàm số bậc nhất trong toán học. Hy vọng khi đọc bài này, các bạn sẽ củng cố được tư duy và định hướng khi giải các bài tập liên quan dạng này. Bạn cũng có thể biết thêm nhiều thông tin quan trọng khác bằng cách đọc các bài viết khác trên trang của giasudiem10. Chúc các bạn luôn học tốt!